Estudio de las secciones cónicas. I Parte: Circunferencia y Parábola

Saludos amigos de hive.

En esta ocasión quiero compartir con ustedes una serie temática de dos capítulos acerca de las secciones cónicas, teniendo en cuenta que esta parte de la geometría analítica es muy importante para poder abordar ciertas superficies cuádricas como paraboloides hiperbólicos, paraboloides elípticos, hiperboloides de una y dos hojas, elipsoides, esferas, cono elíptico, en fin es importante el conocimiento de estas secciones cónicas para poder abordar ciertas gráficas en tres dimensiones que van a depender en gran manera del estudio de las secciones cónicas.

INTRODUCCIÓN

Las cónicas pueden llamarse secciones cónicas ya que son un conjunto de diferentes cuerpos geométricos que poseen algo en común, y no es más que todas las secciones cónicas pueden describirse bajo un efecto de conceptualización como la ocurrencia o existencia de cualquiera de ellas dado que si se intercepta un plano y un cono de dos hojas se genera las cuatros secciones cónicas básicas que son:
- Circulo.
- Elipse.
- Hipérbola.
- Parábola.

Cabe destacar que en esta intersección del plano con el cono de dos hojas el plano no pasa por el vértice del cono, sin embargo cuando se da la circunstancia de que el plano se intercepta con el vértice la figura geométrica que resulta de esta intercepción es una cónica degenerada como las que se muestran a continuación:

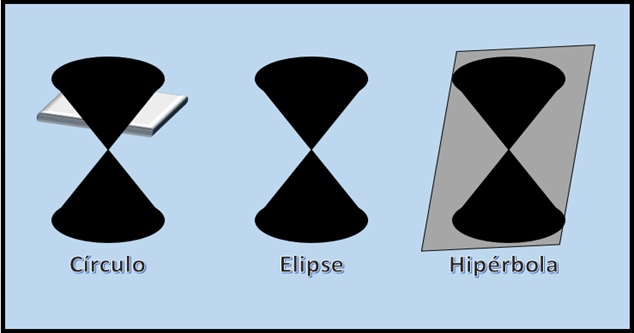
En el caso que se corte un plano con el vértice del cono de dos hojas no va a generar ningún cuerpo geométrico sino que lo que se va a generar es la noción más básica que se conoce dentro de la geometría como lo es el punto.

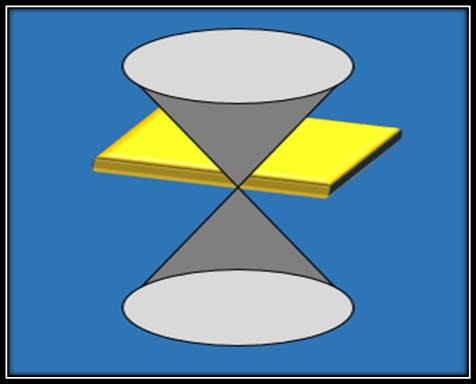
Como hemos podido ver hasta estos momentos con la descripción ya explicada de la intercepción de un plano con un cono de dos hojas, es la forma en la que los griegos introdujeron definieron las secciones cónicas en términos de intercepciones entre el plano y el cono de dos hojas, sin embargo buscando otras alternativas que se fueron desarrollando con el aprendizaje y el conocimiento del álgebra se pudo llegar a una descripción netamente algebraica en la que todas estas secciones cónicas pueden deducirse a partir de la siguiente ecuación de segundo grado:

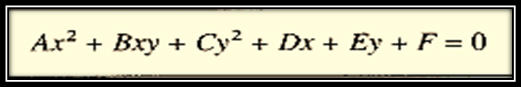
Ya hemos visto estos dos enfoques sobre las cónicas, es decir el de la intercepción de un cono de dos hojas con un plano y el abordaje algebraico deduciendo las secciones cónicas a partir de la ecuación de segundo grado mostrada anteriormente, sin embargo es importante resaltar que existe un tercer enfoque en el que puede ser visto y evaluada las secciones cónicas, esta tercera forma de entender las secciones cónicas es generando un concepto cuya definición sea en la que se tenga que asumir a las secciones como un lugar geométrico en el que un conjunto de puntos satisfacen cierta propiedad geométrica.

Las diferencias existentes para que ese conjunto de puntos satisfagan una propiedad geométrica en particular dan lugar a diversas definiciones, en las que por ejemplo se tiene el de la circunferencia, en la que se puede entender la siguiente definición:

Circunferencia

“Una circunferencia es la agrupación de un conjunto de puntos (x,y) del plano cartesiano que cumplen con el requisito primordial de equidistar de un punto fijo de coordenadas (h,k)”.

A pesar de que esta tercera visión de conceptualización de las cónicas como un lugar geométrico es la que mejor se adapta para su comprensión, no podemos obviar la contribución que puede llegar aportar el álgebra en esta tercera visión, ya que por medio de un análisis algebraico la definición de circunferencia como parte de un lugar geométrico nos conduce a la ecuación canónica de una circunferencia, tal y como se muestra a continuación:

Todo este abordaje me lleva a tomar la decisión de elaborar el abordaje de las secciones cónicas desde el punto de vista de lugar geométrico, para el caso de la circunferencia voy a poner el siguiente ejemplo:

Supongamos que el punto fijo del plano (h,k) de donde va a equidistar el conjunto de puntos (x,y) va hacer el punto (h,k) = (0,0) es decir el origen y r (radio) es igual a 2, esto nos dará una circunferencia de radio 2 cuya ecuación canónica es la siguiente:

Si sacamos la cuenta de sustituir el punto fijo (h,k) = (0,0) y r=2 nos queda la siguiente ecuación canónica:

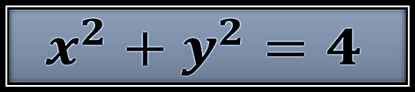
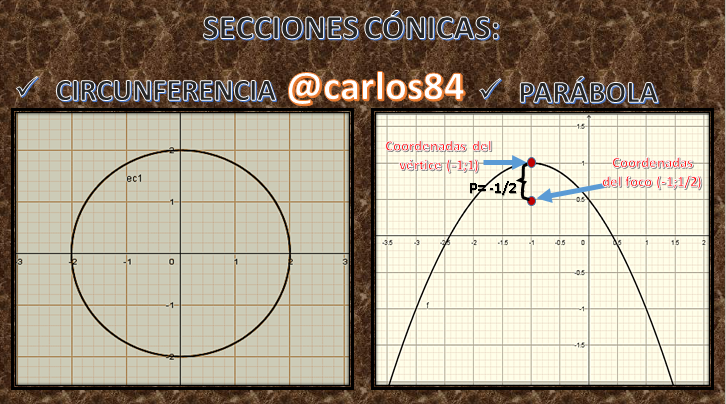
La gráfica de esta circunferencia es una circunferencia de radio 2 y que corta al eje x en X1= 2 y X2 = -2 y al eje y lo corta en y = 2 y y = -2.

Para que se puede visualizar la gráfica con cierto sentido estético quiero usar el software geogebra 5.0 para mostrar la gráfica de la circunferencia:

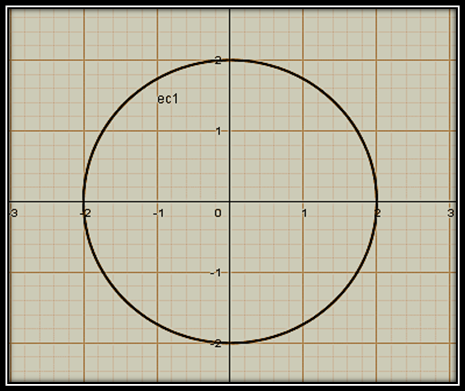
Bajo este enfoque quiero explicar las tres secciones cónicas restantes, ahora le toca el turno de la parábola:

Parábola

De manera similar a la circunferencia podemos definir a la parábola como el conjunto de todos los puntos (x,y) que equidistan de una recta fija llamada directriz y no un punto fijo llamado foco que no pertenece a las coordenadas de puntos de esa recta. La diferencia que para este caso yo consigo entre la parábola y la circunferencia como conceptualización es que la circunferencia el conjunto de puntos del plano (x,y) equidistan de un punto fijo, mientras que la parábola los puntos del plano (x,y) equidistan de una recta llamada directriz a parte de un punto fijo llamado foco, por lo que pudiera decir que el cuerpo geométrico resultante debería ser un poco más complejo para graficar que el de la circunferencia, de todas maneras es necesario continuar con el estudio para sacar conclusiones entre la complejidad de estos cuerpos geométricos llamados secciones cónicas.

Para considerar la ecuación canónica de la parábola hay que considerar el vértice de la parábola que no va hacer más que un punto de coordenadas (h,k). También hay que considerar la recta directriz y = k-p. La ecuación canónica de la parábola va a diferir dependiendo de si el eje de la parábola va hacer vertical o horizontal, para el caso del estudio que voy a contemplar solo voy a considerar cuando el eje es vertical, ya que cuando el eje es horizontal la parábola abre sobre el eje x, y esto para el estudio de funciones no es idóneo, ya que una parábola que abra sobre el eje x no es una función, ya que para cada valor de x le corresponde dos valores de y, cabe destacar que desde el punto de vista geométrica una parábola siempre será una parábola independientemente si abre sobre el eje x o sobre el eje y.

Ecuación canónica de la parábola cuando abre sobre el eje Y (Eje vertical)

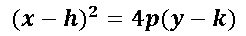
Para realizar un estudio respectivo acerca de la definición canónica de la parábola quiero explicar el siguiente ejemplo:

Graficar la parábola cuya ecuación es:

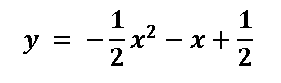
Para graficar este parábola simplemente habría que aplicar la misma metodología para graficar una parábola como se hace en cálculo I, es decir encontrando los cortes con los ejes coordenados, sin embargo a modo de simplificar, voy a introducir esta ecuación de segundo grado en el software geogebra 5.0 y a extraer el gráfico y mostrárselos a continuación:

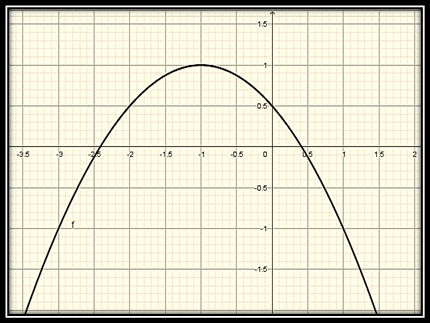
Para este caso la recta directriz es el eje x. El vértice de la parábola tiene coordenadas (1,-1) y para saber las coordenadas del foco es necesario calcular las coordenadas de este punto (h, k + p), de lo que se puede deducir que de las coordenadas del punto focal la coordenada en x=h y las coordenadas en y= k+p, por lo que podemos concluir que para calcular las coordenadas del punto focal es necesario saber el valor de h, k y p. Para calcular los valores de h, k y p realizamos la completación de cuadrado de la ecuación cuadrática:

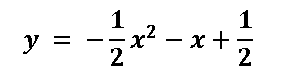
La completación de cuadrado de esta ecuación cuadrática es:

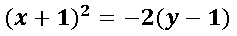
Esta completación de cuadrado se asemeja a la ecuación canónica de la parábola cuando abre sobre el eje y (eje vertical):

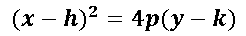
Donde h = -1 y k = 1. Para calcular el valor de p nos planteamos la ecuación de la recta directriz y = k-p lo que implica que p = k –y, y por el gráfico de la parábola sabemos que corta a y en 0,5 entonces y=1/2 y k= 1, se sustituyen los valores de y y k para conseguir p, por lo tanto p= 1-1/2 lo que implica que p=1/2 pero como la parábola abre hacia abajo implica que p = -1/2.

Puesto que la parábola abre hacia abajo su foco está a p unidades del vértice, por lo que las coordenadas del punto focal serán:

(h, k+p) lo que implica que k+p = y y h = x.k+p= 1-1/2 implica que k+p= 1/2.

Las coordenadas del punto focal es (-1, 1/2)
A continuación les presento la imagen del gráfico elaborado con geogebra 5.0 con todas las características ya explicadas como las coordenadas del vértice y del punto focal:

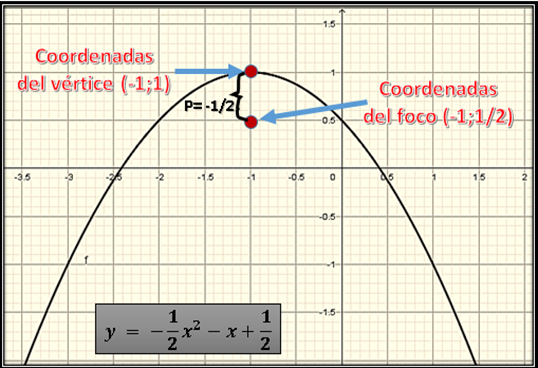
Conclusión y consideraciones

Si estudiamos toda la evolución histórica que tuvo las secciones cónicas en sus inicios podemos evaluar que la mejor forma de entender las secciones cónicas es mediante la definición de lugar geométrico, también el álgebra forma parte importante para comprender el gráfico y el comportamiento de estas secciones cónicas, ya que mediante el estudio algebraico tenemos la posibilidad de plantearnos por ejemplo las diferentes formas de expresar la ecuación canónica de estas secciones cónicas, también el estudio algebraico nos permite calcular los puntos focales y vértices de las diferentes secciones que son muy comunes entre sí.

Es importante poseer una herramienta de ayuda, ya que la tecnología nos proporciona de las herramientas que nos facilita la forma en la que podemos representar el gráfico de muchas de estas secciones cónicas, es por ello que elegí utilizar el software geogebra 5.0 para plantearme una opción bastante viable de graficar y evaluar el comportamiento de ciertos gráficos que fueron ejemplos para complementar la parte teórica en la definición y características de cada sección cónica.

Nota: Todas las imágenes son de mi autoría y fueron elaboradas utilizando las herramientas de Microsoft Power Point. Las ecuaciones y ejemplos mostrados fueron elaborados empleando las herramientas de inserción de ecuaciones de Microsoft Word.

Referencia consultada y recomendada