Learn how to use recursion in JavaScript
Recursion can be very confusing the first time you come across it (you will find out why later) but it can be a very useful tool if you can understand how it works and how to use it. But before I go on, what is recursion?

Recursion is simply a technique where a function or any other algorithm calls itself one or more times until a condition has been met. It's a way of breaking a big problem into smaller chunks and solving them individually. A recursive function in JavaScript can look like this:
function sum(n) {
If (n === 0) {
return 0;
}
else {
sum(n - 1);
}
}
To demonstrate how this work, I will use an example gotten from one of the problems I solved in freeCodeCamp's JavaScript course. A friend of mine contacted me a few days ago and said he couldn't solve the same problem and had to take a peek at the solution but he still didn't understand how it works, so I decided to come up with this tutorial as an explanation for those who don't understand how recursions work.
The problem

For example, if we have sum([2, 3, 4, 5], 2), we are to look for the sum of the first 2 numbers in that array which are 2 and 3, so the answer will be 5. In sum([2, 3, 4, 5], 3), it means we should look for the sum of the first 3 numbers in the array which are 2, 3, and 4, the answer will be 9. Let's look at the code that I used to solve this.
function sum(arr, n) {
if (n === 0) {
return n;
}
else {
return sum(arr, n - 1) + arr[n - 1];
}
}
result = sum([2, 3, 4, 5], 3);
console.log(result);
The first thing I did is to set up a base condition or case where the function will stop calling itself. If you don't set up a base case, the function will just keep calling itself until the program crashes (sort of like an infinite loop). The base case simply checks if n is equal to 0, and then if n is 0, it returns it to the caller of the function. That's simple enough.
Else if n is not equal to 0, then we need to keep reducing it until it eventually becomes 0 and executes that base case. That's why we have the sum(arr, n -1) there, it will call the same function again but this time, n will be reduced by 1. Whenever a function is called, it gets added to something called a call stack, and this is what it looks like

Each of those functions needs to be executed from the top (sum) to the bottom (). If the first function call at the top isn't executed, the second one won't get executed, it will wait for the first one to finish before it moves forward. The last function call at the bottom is and it represents the first place we called the function which is result = sum([2, 3, 4, 5], 3).
The call stack process
1. The sum(arr, n) function is called and arr becomes [2, 3, 4, 5] while n is 3. This gets added to the stack

arr = [2, 3, 4, 5]
n = 3
Since n isn't equal to 0, we skip the if statement and go to the else.
return sum(arr, n - 1) + arr[n - 1]; // ignore + arr[n - 1] for now
// this simply means
return sum([2, 3, 4, 5], 2);
The code is paused at this point and we execute the next function call which is now sum([2, 3, 4, 5], 2). This gets added to the stack.

Now the red function will have to wait for the green one to finish executing before it can move forward.
2. arr = [2, 3, 4, 5]
n = 2
n is still not equal to 0, so we go to the else statement.
return sum(arr, n - 1) + arr[n - 1]; // ignore + arr[n - 1] for now
// this simply means
return sum([2, 3, 4, 5], 1);
The code is paused at this point and we execute the next function call which is now sum([2, 3, 4, 5], 1). This gets added to the stack
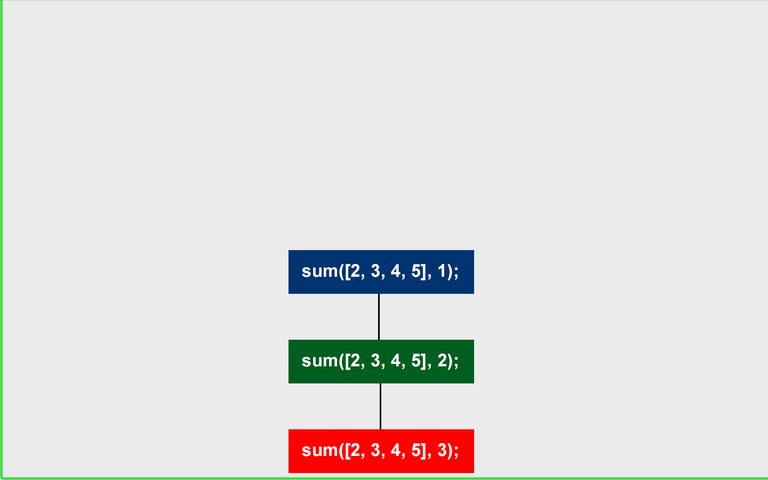
3. arr = [2, 3, 4, 5]
n = 1
n is still not equal to 0, so we go to the else statement.
return sum(arr, n - 1) + arr[n - 1]; // ignore + arr[n - 1] for now
// this simply means
return sum([2, 3, 4, 5], 0);
The code is paused at this point and we execute the next function call which is now sum([2, 3, 4, 5], 0). This gets added to the stack

4. arr = [2, 3, 4, 5]
n = 0
n is now equal to 0, so we can now execute the if statement.
return n
We can also say return 0, it's the same thing.
0 is now sent back to the place where this function was called.
Returning from the call stack
Now we have gotten to the base case and we no longer have to make any function calls, it's time to start going back. Each of those function calls in the call stack will have to be returned starting from the first one which is sum([2, 3, 4, 5], 0). 0 is the value we are returning from this function, and that value will be sent back to the position where this function was called.

Once the value has been returned, we are finally done with this function and it is removed from the stack, the next function in line is now the blue one. If you look back, you will see that the sum([2, 3, 4, 5], 0) function was called in step 3 and that's exactly where we will continue from.
3. arr = [2, 3, 4, 5]
n = 1
return sum(arr, n - 1) + arr[n - 1];
// this simply means
return sum([2, 3, 4, 5], 0) + arr[0];
sum([2, 3, 4, 5], 0) will now be replaced with 0.
arr[n - 1] becomes arr[0] which means the first item in that array, and it is 2. So we now have:
return 0 + 2 which is just return 2.
2 becomes the value we are returning from this function, it will be sent back to the position where this function call was made (step 2). And with that, we are done with the blue function and it will be removed from the stack. The next function in line is now the green one.
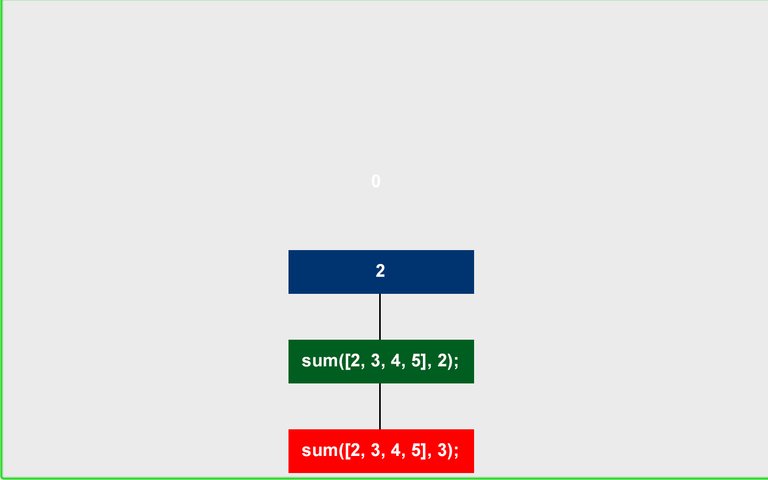
2. arr = [2, 3, 4, 5]
n = 2
return sum(arr, n - 1) + arr[n - 1];
// this simply means
return sum([2, 3, 4, 5], 1) + arr[1];
sum([2, 3, 4, 5], 1) will now be replaced with 2.
arr[n - 1] becomes arr[1] which means the second item in that array, and it is 3. So we now have:
return 2 + 3 which is just return 5.
The value is sent back to the position where this function was called (step 1) and the green function is removed from the stack and we fall back to the red one.

1. arr = [2, 3, 4, 5]
n = 3
return sum(arr, n - 1) + arr[n - 1];
// this simply means
return sum([2, 3, 4, 5], 2) + arr[2];
sum([2, 3, 4, 5], 2) will now be replaced with 5.
arr[n - 1] becomes arr[2] which means the third item in that array, and it is 4. So we now have:
return 5 + 4 which is just return 9.
The value is sent back to the position where this function was called and that was result = sum([2, 3, 4, 5], 3).
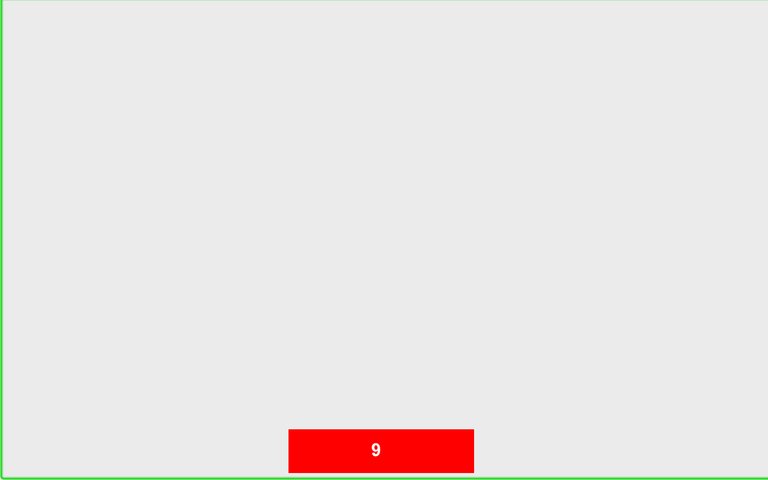
So, when we do 'console.log(result)', 9 will be the output we will see on the console.
It can get confusing
If you look back at all the steps, you will see that we were just doing the same thing over and over again. Step 1, 2, 3 are basically the same things been done repeatedly, and step 3, 2, 1 is just us returning from the first 3 steps and we did basically the same thing in all of them. Something like this can get very confusing and complicated when you're dealing with a very large amount of data.
If you're using recursions, the best approach is to use a small set of data to run tests. Instead of doing something like sum([2, 3, 4, 5, 6, 7, 8, 9,], 6) as a test to keep track of your statements, you should instead use something smaller like sum([2, 3, 4], 2). Why I am saying this is because as a beginner, you will likely have to draw a stack and write out each function call process just so you wouldn't get confused and that will be easier to do if you're using a small data set.
Recursion is just an alternative for loops and you can choose to continue using loops because it's less complicated than this. The only reason some people like using recursions is because it's more elegant to write (and probably to show off) but it isn't memory efficient as each of the function calls will require space on the stack.
This same problem I solved with recursions can be done with loops and it is quite easy to understand when compared to the recursive method.
function sum(arr, n) {
let counter = 0;
for (let i = 0; i < n; i++) {
counter += arr[i];
}
return sum;
}
result = sum([2, 3, 4, 5], 3);
console.log(result);
I personally prefer the loop method, at least I didn't need to start thinking of a base case or start walking through each call stack. Why then should you learn recursions? You should learn it because of coding interviews, some companies will give you a problem and tell you to solve it using recursions and one of the popular recursion problems asked in coding interviews is the Fibonacci sequence number
Thanks for reading

Connect with me on:
Twitter: @kushyzeena
Readcash: @kushyzee
Congratulations @kushyzee! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 900 comments.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
I know the Fibonacci Sequence, but not the coding process. It seemed challenging!
I recently came across and it was complicated at first but once I understood how it works, it became easier. It's quite interesting 😊
The main reason why I abandoned programming.. Too complicated 🤣
😂 I sometimes feel like giving up on it but I always remember that success doesn't come easily, it's a complicated process 😁
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
I've always used loops to solve problems like this and I think they're still what I prefer but recursions are new to me and this article did open a new JavaScript thinking gateway for me😊.
Thanks for sharing!
I only use loops too but it's good to know about recursions just in case an employer asks you to solve a problem using it
https://twitter.com/kushyzeena/status/1574007216889384960
The rewards earned on this comment will go directly to the people( @kushyzee ) sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
They love to use fibonacci sequence in questions lol
!1UP
They certainly do, a lot of people said they have come across it. Thanks for the tokens 😊
You have received a 1UP from @gwajnberg!
@oneup-curator, @stem-curator, @vyb-curator, @pob-curator, @neoxag-curator, @pal-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
Great work bro. Following you on twitter now
Thanks for the follow 😊
Thank you for sharing this amazing post on HIVE!
Your content got selected by our fellow curator @tibfox & you just received a little thank you via an upvote from our non-profit curation initiative!
You will be featured in one of our recurring curation compilations and on our pinterest boards! Both are aiming to offer you a stage to widen your audience within and outside of the DIY scene of hive.
Join the official DIYHub community on HIVE and show us more of your amazing work and feel free to connect with us and other DIYers via our discord server: https://discord.gg/mY5uCfQ !
If you want to support our goal to motivate other DIY/art/music/homesteading/... creators just delegate to us and earn 100% of your curation rewards!
Stay creative & hive on!