Relation between angle bisectors of two angles and the third angle of a triangle

Hello maths bugs(🐞) and hivers(🐝)
I hope you are strong & stout and doing good in life.

Well come back to another interesting tropic.It's about the angle made by any two bisectors of internal angle and also the third angle of any kind of triangle as you can see in the following figure.

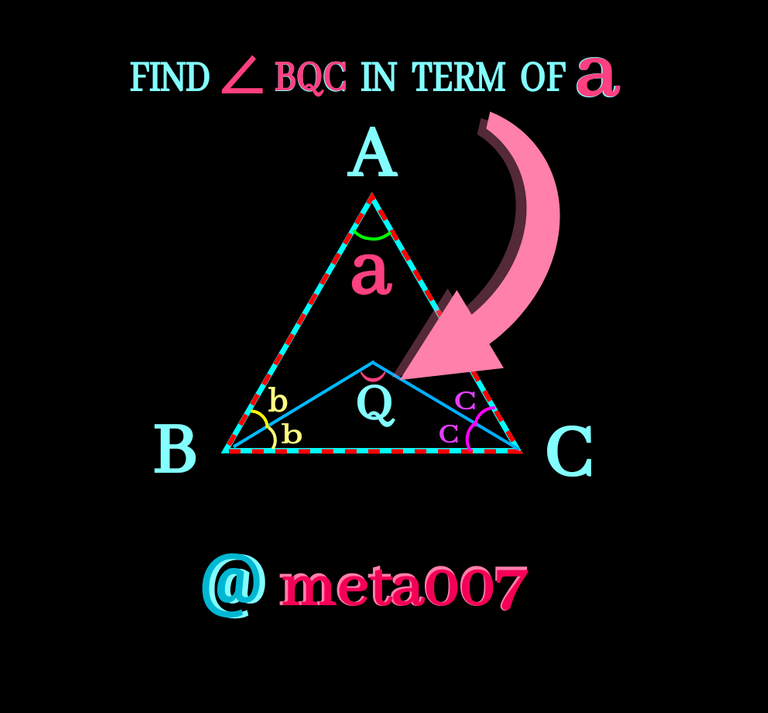
Before coming to the main point, I just wan to remind you a very important property of a triangle.Sum of three angles of a ∆ is 180. In the following figure you can check it.In the figure given below I wrote down the property in both cases of ∆.

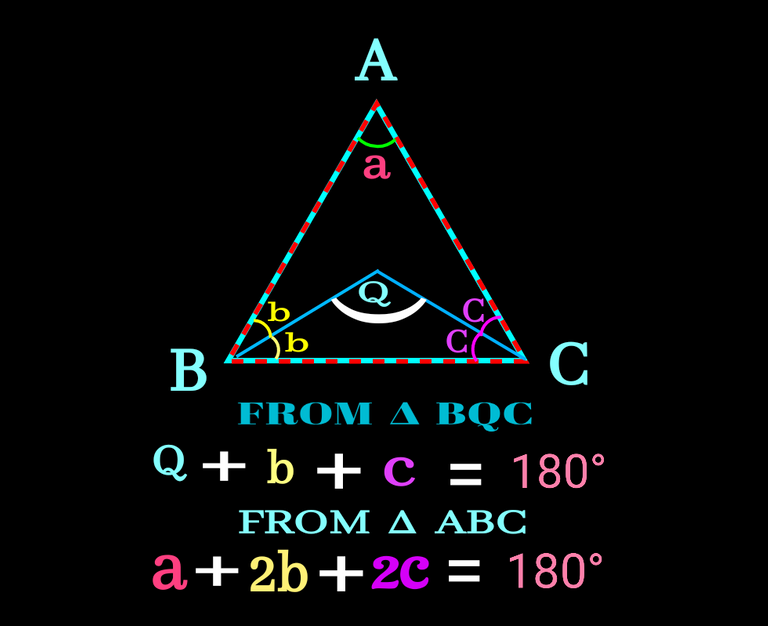
Value of ∠b and ∠c from any of the two equation in previous figure need to put in the other equation.Here I find the value of the two angle using larger ∆ABC and put it in the angle sum property of the smaller triangle. You can check it where I put the sum of ∠b and ∠c

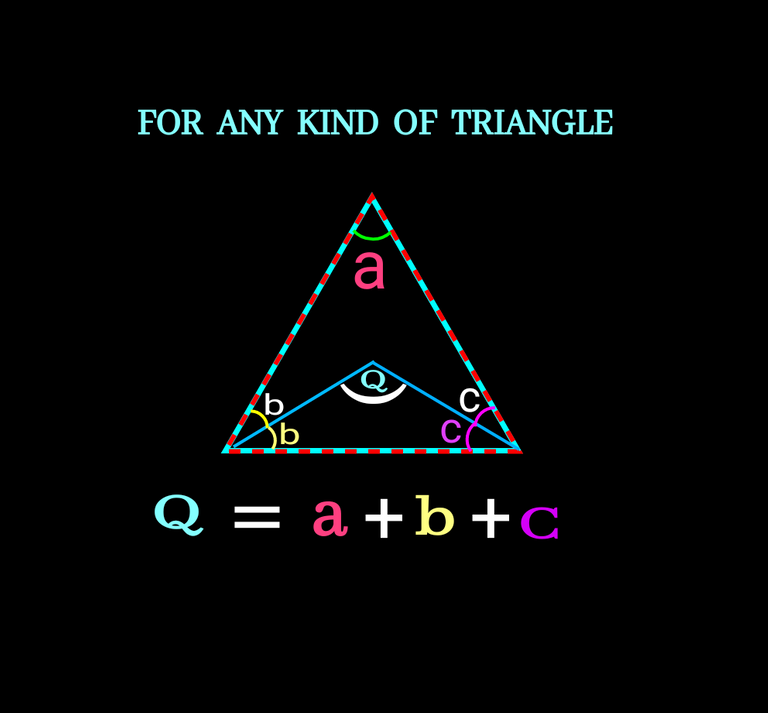
The value we find from a+2b+2c= 180° is 90°-a/2 and then when we put the value we have just found in Q+n+c=180°.After solving further, we find the value of It's very simple check it below.

In the figure above the second line come after dividing the first equation by two and then we took a/2 to the RHS of the equation and thus we find sum of angle b and c.Then In the next equation we replace (b+c) and switch side to get the value of Q.

For any kind of triangle it is true. You can also satisfy yourselves by taking different value of angles. For any value of angle even if you take an imaginary angle like zero ,the property will also exit but angle-sum of a triangle must be 180°.

Points to be considered:

✅✅There are two kind of bisectors. 1) internal angle bisectors of a triangle and 2) external angle bisectors of a triangle.

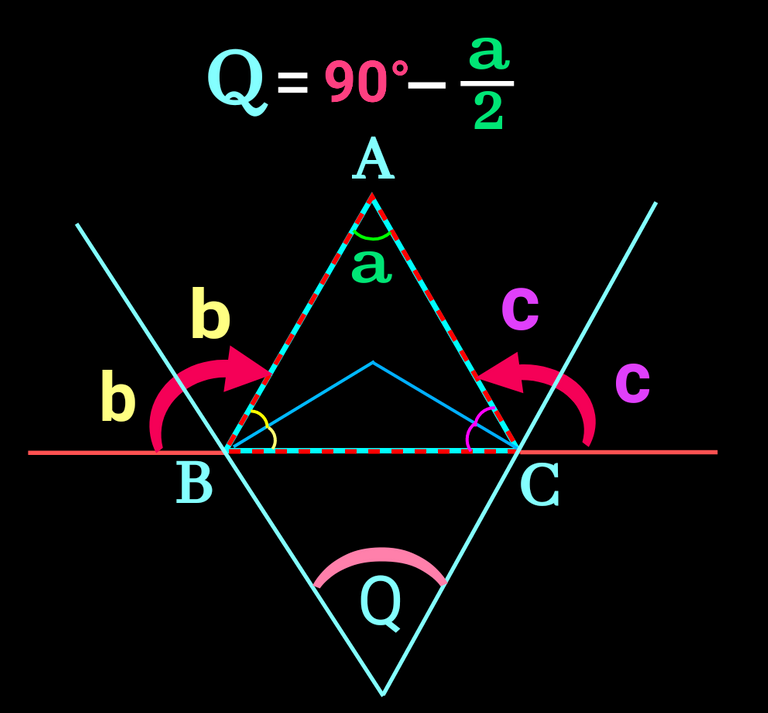
✅✅ Here The formula Q=90°+a/2 is for the first case i.e internal bisectors.

✅✅ For the external bisectors the formulla will be Q=90°-a/2.The figure looks like as below:

I hope you find my article worth reading.

Thanks for stoping by.

See you around.

All is well

Regards: @meta007