Análisis estructural de arco circular
Realizaremos el análisis estructural de un arco circular simplemente apoyado, sometido a dos cargas externas. En la anterior publicación, se realizó lo mismo para un arco parabólico, en donde primero se hallaron sus parámetros geométricos para luego calcular fuerzas (parámetros estructurales).
El ejercicio a realizar en esta ocasión se da en la siguiente figura:
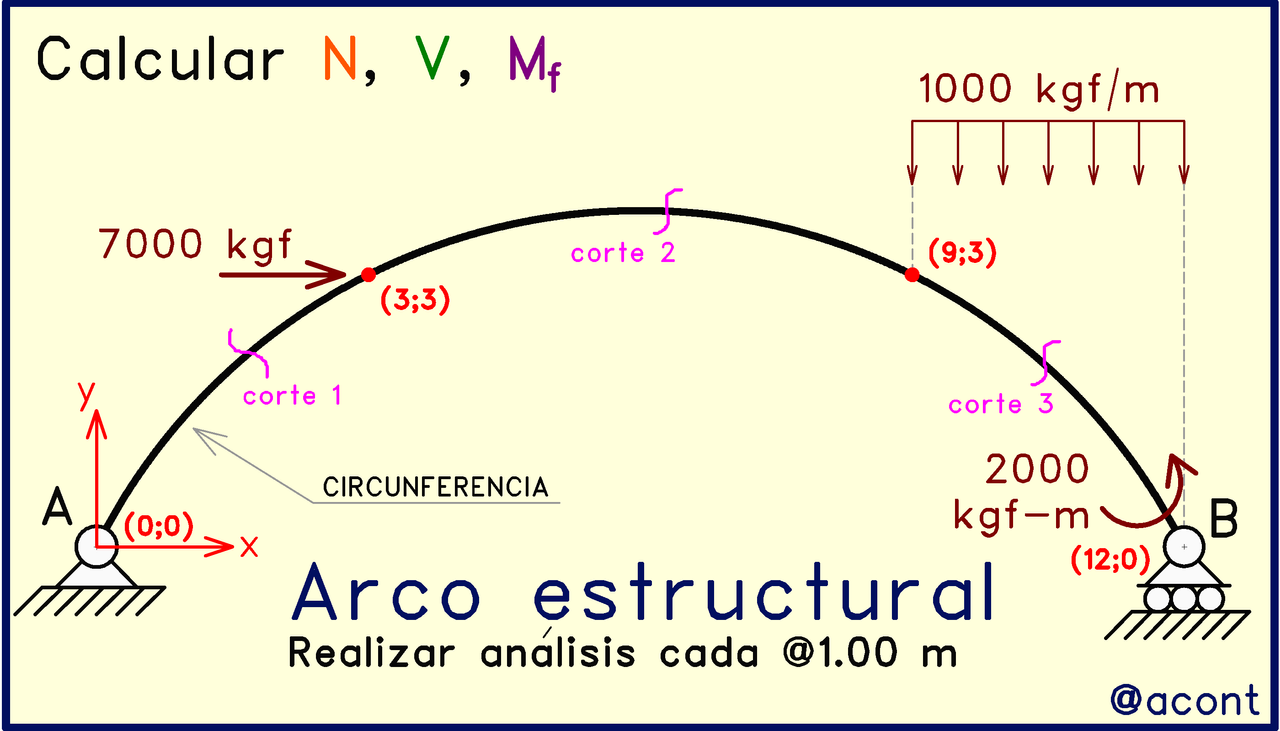
Se muestra un arco con distintas coordenadas en donde se ubican distintos puntos de interés que utilizaremos luego para hallar la función matemática que describe al arco. El arco está sometido a tres cargas externas, de las cuales dos se encargan de dividir el arco en tres sectores o tramos.
Geometría
Primeramente, encontraremos la función matemática que describe la forma del arco. La ecuación de una circunferencia posee tres parámetros (coordenadas “xo” y “yo” del centro, y el radio “R”, los cuales determinaremos a partir de las coordenadas dadas:

Con tres de las coordenadas podemos determinar un sistema de tres ecuaciones con tres incógnitas, el cual una vez resuelto, nos lleva a la función matemática deseada. Cabe destacar que no siempre tendremos un punto de coordenadas (0;0) en el arco, puede que el arco esté compuesto por diferentes funciones matemáticas y una de ellas no pase por dicho origen.
Cálculo de reacciones externas
Empleando las ecuaciones de equilibrio estático, podemos calcular las reacciones externas del arco:

Cálculo de reacciones internas
Para el cálculo de las reacciones internas (generales, en horizontal y vertical), debemos analizar la configuración de las cargas externas y determinar los puntos de discontinuidad. De esta manera, podemos conocer cuentos tramos tenemos y, por lo tanto, cuantos cortes debemos realizar.
Estos “tramos” o “intervalos” se determinan siempre en el eje horizontal, a menos que sea más cómodo hacerlo en vertical, en caso de que el arco tenga diferente disposición.
La fuerza puntual de 7000 kgf es un punto de discontinuidad, ya que en dicho punto existirá un salto en la magnitud de las solicitaciones, es decir, discontinuidad en los diagramas de solicitaciones, en caso de dibujarse sobre el arco. Este punto determina el fin del primer tramos e inicio del segundo.
Seguimos sin ninguna interrupción hasta llegar al inicio de la carga distribuida uniforme de 1000 kgf/m, la cual introduce nuestro segundo punto de discontinuidad. Tenemos entonces un segundo tramo el cual abarca la parte superior del arco.
Desde el punto donde inicia esta carga distribuida hasta el punto final del arco (si observamos de izquierda a derecha), no existen discontinuidades, ya que dicha carga distribuida se mantiene uniforme hasta el punto donde se encuentra el patín (articulación móvil en “B”). Cabe destacar que el momento externo de 2000 kgf-m al encontrarse aplicado en el extremo (al final del arco) no introduce discontinuidad y es un valor de referencia que podremos verificar más adelante.
Corte 1-1
En el primer tramo, obtenemos el siguiente subsistema:
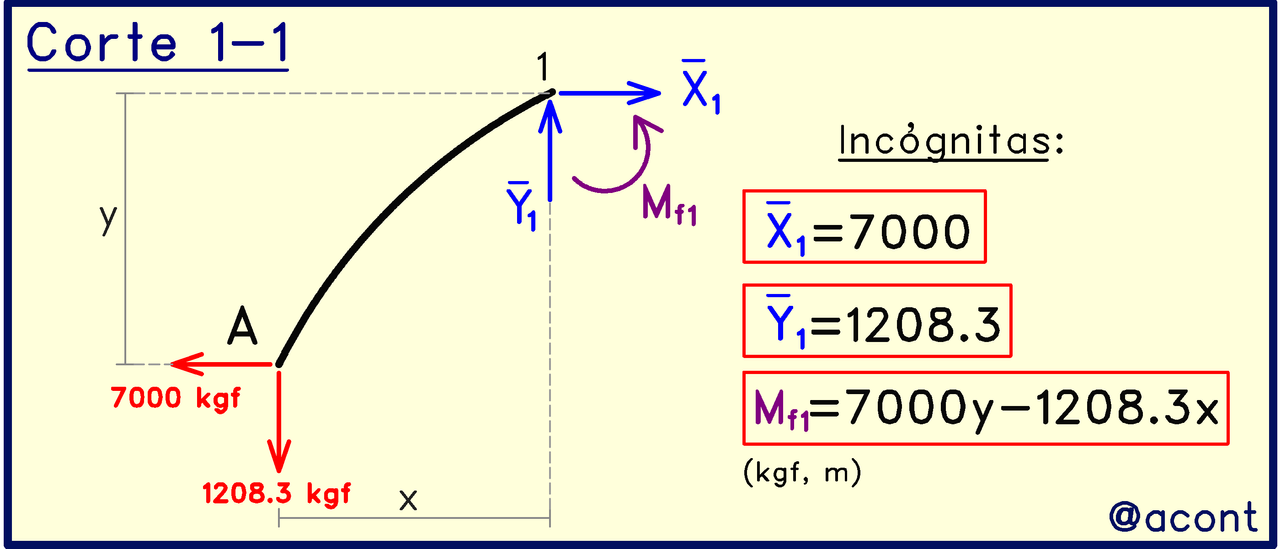
Al igual que en la publicación anterior, colocaremos distancias genéricas “x” y “y” referentes al origen de coordenadas del arco. Con esto podemos hallar la ecuación de las fuerzas horizontal, vertical y de momento flector en un punto genérico del tramo. Se expresaron las ecuaciones respectivas directamente obtenidas a partir de las ecuaciones de equilibrio estático.
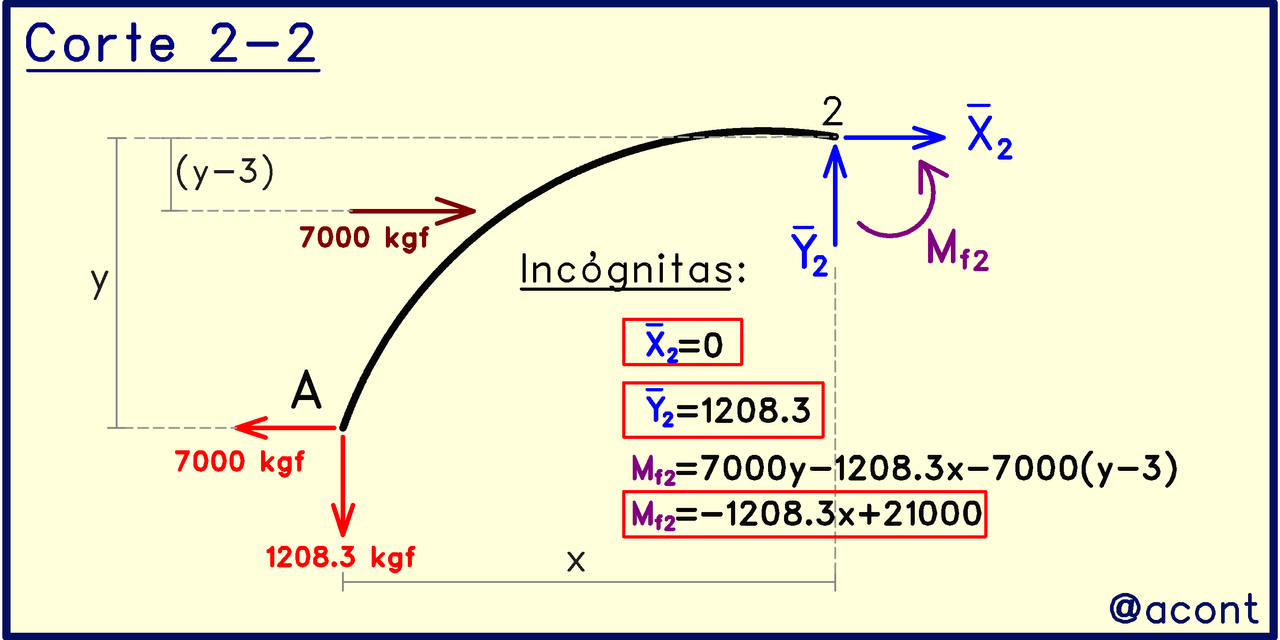
Corte 2-2
Esta vez se puede apreciar en el corte la carga puntual horizontal de 7000 kgf. El resultado de aplicar las ecuaciones de equilibrio estático es el siguiente:
Corte 3-3
En este corte, aparecerá una porción genérica de la carga distribuida, dicha distancia la expresaremos en función de “x” a partir del origen del arco y las coordenadas conocidas.
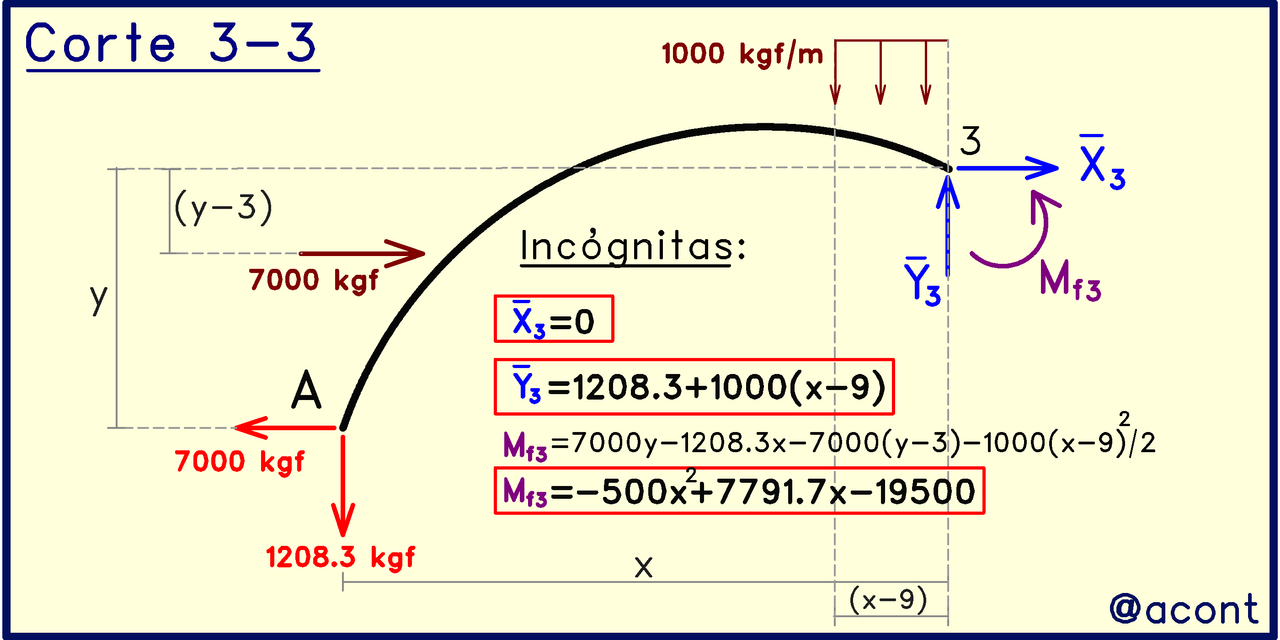
Podemos notar que el momento externo de 2000 kgf-m no aparece por ninguna parte en estas ecuaciones y cortes, ya que es un valor que deberíamos poder comprobar al evaluar la ecuación hallada para el momento flector en el tercer tramo para x=12 m, lo cual representa el punto final del arco.
Estas ecuaciones se encuentran reflejando las fuerzas internas en un sistema general (horizontal-vertical). Al igual que en el ejemplo de la publicación anterior, debemos proyectar dichas fuerzas a un sistema de ejes locales (tangente-perpendicular al arco). De esta manera, encontramos las fuerzas axiales y cortantes que actúan en el arco.
Ecuaciones de transformación geométrica
En esta publicación se puede encontrar las ecuaciones necesarias para realizar los cálculos de las solicitaciones de fuerza axial y cortante en un arco, en función de las fuerzas internas horizontales y verticales:

La derivada de la función que define al arco es:

De esta manera podemos establecer ecuaciones para las fuerzas axial y cortante en cada tramo en función de las distancias “x” y “y”:

Cálculo de solicitaciones
Construiremos una tabla que muestre el valor de las solicitaciones en el arco cada @1.00 metros tal como dice el enunciado. Agregaremos una columna con el valor de “y” el cual varía según la función matemática hallada. También añadiremos una columna para la derivada y’=f’(x).
Utilizaremos una hoja de cálculo para realizar el cálculo de las solicitaciones en una tabla, que expresa el valor de N, V y Mf, solicitaciones que debemos hallar para completar el análisis estructural:
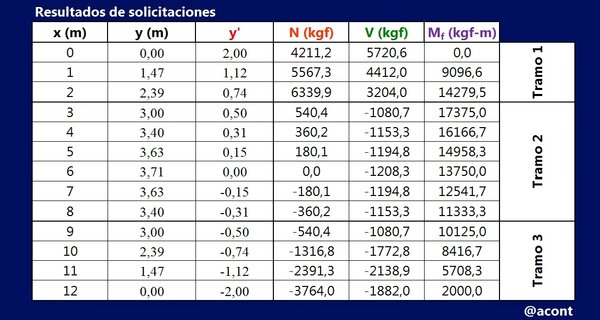
Análisis de los resultados
Analizando los resultados de solicitaciones obtenidos, podemos observar que los valores de fuerza axial son positivos en la primera mitad del arco, indicando que dicho sector está sometido a fuerzas de tracción.
Aunque los arcos suelen trabajar a compresión, puede darse el caso donde la configuración de las cargas externas induzca lo contrario, tal como es el caso de la fuerza puntual de 7000 kgf, la cual posee una magnitud considerable y genera tracción en la primera mitad debido a su orientación, en contraste con la otra mitad en donde la carga distribuida genera compresión ya que se orienta hacia abajo.
La fuerza puntual de 7000 kgf tiene un efecto bien marcado en la magnitud de las fuerzas cortantes. Las fuerzas de corte empiezan siendo positivas en el primer tramo, hasta que aparece la fuerza puntual y debido a su magnitud y sentido, cambia el signo de las fuerzas obtenidas en la tabla. Esta fuerza puntual induce un salto de aproximadamente 4000 kgf en las fuerzas de corte.
Tal como se ha mencionado en anteriores publicaciones, los valores máximos/mínimos del momento flector se dan en los puntos donde la fuerza de corte es nula. Esto se refleja en la primera discontinuidad (la fuerza puntual de 7000 kgf), ya que el salto en el diagrama de corte se da de un valor positivo a negativo, pasando por cero en el proceso. Por ello, el valor de 17375,0 kgf-m es mayor a los valores adyacentes.
Finalmente, se comprueba que el valor final del momento flector obtenido mediante la ecuación del tercer tramo es 2000 kgf-m, lo cual concuerda con lo que se observa en la imagen del arco. Si este momento externo de 2000 kgf-m no existiese, el valor final del momento flector en la tabla sería nulo, al menos que en el punto final se encuentre un vínculo que restrinja la rotación, como es el caso de un empotramiento.
Aportes de esta publicación
| Se presenta el abordaje práctico de un arco estructural que sigue la función de una circunferencia. Se calculan las solicitaciones que actúan en el arco debido a las cargas externas y se realiza un análisis de los resultados obtenidos. Esta publicación es de utilidad para estudiantes y cualquier persona interesada en el análisis de estructuras con miembros curvos y la metodología empleada para abordarlos, en asignaturas como Estática Aplicada o cualquiera que implique estudiar estructuras con estas características. |
Referencias
[1] Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 124-133).Fuente
Material recomendado
•Análisis estructural de miembros curvos
•Análisis estructural de arco parabólico
Imágenes de autoría propia realizadas mediante LibreCAD y PowerPoint.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
Atentamente
EQUIPO ENLACE 2020
Muchas gracias Proyecto Enlace, saludos y éxitos.
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 4 de octubre del 2020 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 HIVE transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
2. Contáctanos en Discord: https://discord.gg/hkCjFeb
3. Suscríbete a nuestra COMUNIDAD y apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Saludos al equipo de Entropía y gracias por su valoración!
Excelente publicación, gracias por compartir.
Muchas gracias por tu comentario, saludos.
Interesante y muy buena publicacion amigo, no entendí al 100% porque no soy tan bueno en matemática ni geometría jajaja pero pese a eso entendí lo suficiente de la variables de la fuerza axial y un poco de la fuerza de tracción y las reacciones internas como externas, sería interesante ver esto con la serie de publicaciones que has hecho en estos días para un conversatorio uwu. Saludos y feliz día amigo, espero seguir nutriendo más contigo de a poco en la ingeniería civil.
Saludos @memes777 gracias por pasar y comentar! Me alegro que hayas entendido, traté de simplificar el abordaje matemático para que sea más claro. No descarto realizar un conversatorio más adelante sobre algún tema. Saludos y feliz día!
Lo espero con ansías amigo.