Geometría Descriptiva mediante SketchUp Parte VI: intersección de planos

Saludos a todos y bienvenidos a la presente publicación. Determinar la intersección entre un plano y una recta o entre dos planos suele ser una práctica frecuente en problemas de Geometría Descriptiva, es por ello que esta publicación va enfocada a este procedimiento. Desde luego, se utilizará el programa SketchUp para así generar vistas en el espacio de la situación, facilitando así el entendimiento de los procedimientos utilizados en la doble proyección ortogonal, de manera que el lector interesado en el tema entienda el porqué de cada elemento trazado e incentivando el desenvolvimiento de la comprensión espacial.

Intersección de una recta con un plano

El lugar geométrico de la intersección de una recta con un plano es simplemente un punto. Por lo tanto, la solución al problema será encontrar el punto de intersección de una recta dada con un plano dado. Tal como se observa en la Fig. N°1, se tiene un plano “ab” definido por dos rectas paralelas “a” y “b” y una recta dada “c” y se desea determinar en la doble proyección ortogonal (DPO) la intersección de esta recta con el plano “ab”.

_{Figura N°1}

El plano contiene dentro de sí infinitas rectas, y recordemos de la anterior publicación que podemos determinar de él las que más nos convengan. De esta manera, vamos a determinar una recta adicional dentro del plano dado que se corte con la recta dada justo en el punto que necesitamos conocer. El problema se reduce entonces a determinar el punto de corte entre dos rectas, una dentro del plano y otra fuera de este (Fig. N°2). Pero ¿Cómo determinamos esta “recta adicional”?

_{Figura N°2: la recta “t” se hizo coincidir con la proyección vertical de la recta “c”. La diferencia entre las rectas “t” y “c” radica en que la primera pertenece al plano, mientras que “c” se corta con el plano. Ambas rectas se cortarán en el punto solución.}

En la Fig. N°2, se ha creado una recta adicional “t” dentro del plano, cuya proyección vertical coincide con la proyección vertical de la recta dada “c”. Pero como esta recta adicional “t” se encuentra dentro del plano “ab”, se va a cortar con las otras rectas que también pertenecen al mismo plano (“a” y “b”). En la DPO, estos puntos de corte en la proyección vertical se llevan a la proyección horizontal mediante líneas de referencias verticales hasta las mismas rectas “a” y “b” del plano, de esta manera, obtenemos la proyección horizontal de la recta adicional “t” la cual no coincide con la de “c” y se corta con esta en un determinado punto. Este punto se eleva verticalmente mediante una línea de referencia hasta la proyección vertical de “c” y de esta manera obtenemos las proyecciones del punto solución “P”. Esto se ilustra en la Fig. N°3.

_{Figura N°3}

Lo mismo pudo haberse hecho haciendo que la recta adicional “t” coincida con la proyección horizontal de “c” en vez de la vertical, ejecutando el procedimiento de forma análoga, llegando así al mismo resultado para el punto solución “P” (Fig. N°4).

_{Figura N°4: caso en el que se realiza el mismo procedimiento con la proyección horizontal de la recta “c” llegando al mismo resultado.}

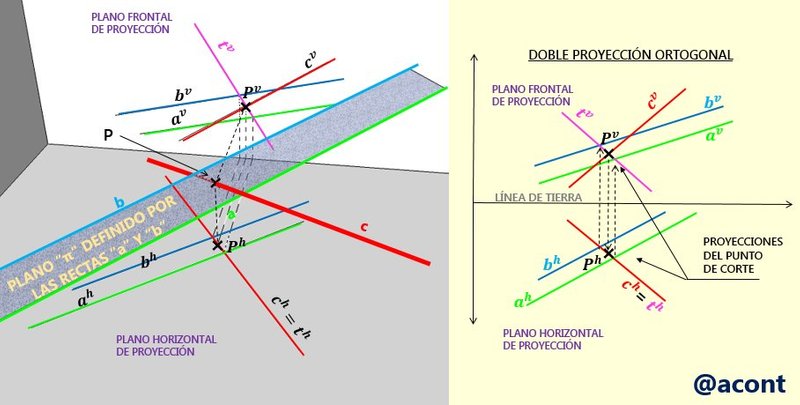
¿Qué sucedería si las rectas “c” y “t” resultasen ser paralelas? En este caso, la recta “c” sería paralela al plano “ab” ya que no existiría punto de corte o el mismo se encuentra en el infinito. ¿Qué sucede si las rectas “c” y “t” coincidieran? La recta “c” no sería una recta fuera del plano “ab” sino perteneciente o coplanar a este, por lo que no existe un solo punto de corte, sino que toda la recta pertenece al plano.

La letra “t” es utilizada por Osers et al. para referirse a la recta adicional “t” como “recta tapada”, ya que esta recta está siendo “tapada” por otra en una de sus proyecciones.

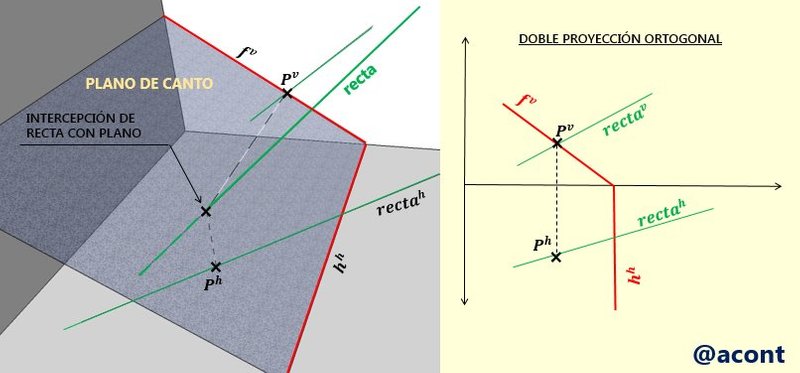
En el caso de los planos de canto y plano vertical (ver publicación anterior, referente a los planos en posiciones particulares), la intersección de una recta cualquiera con estos no requiere de la determinación de una recta adicional, ya que estos planos son totalmente perpendiculares a alguno de los planos de proyección de la DPO, por lo que el punto de corte se mostrará directamente en alguno de los planos de proyección. Esto se entiende mejor, ilustrado en la Figura N°5.

_{Figura N°5}

Intersección entre dos planos

El lugar geométrico de la intersección entre dos planos es una recta, es decir, un número infinito de puntos que ambos planos tienen en común y que están alineados entre sí (Fig. N°6). La única excepción a esta regla se da en dos planos paralelos, los cuales no poseen puntos en común.

_{Figura N°6}

Para determinar esta recta de intersección entre dos planos, nos basta conocer dos puntos sobre la misma. Para ello, debemos tomar dos rectas de uno de los planos y encontrar el punto de intersección de cada una de estas con el otro plano, es decir, se ejecuta dos veces el procedimiento anteriormente explicado para encontrar la intersección de una recta con un punto.

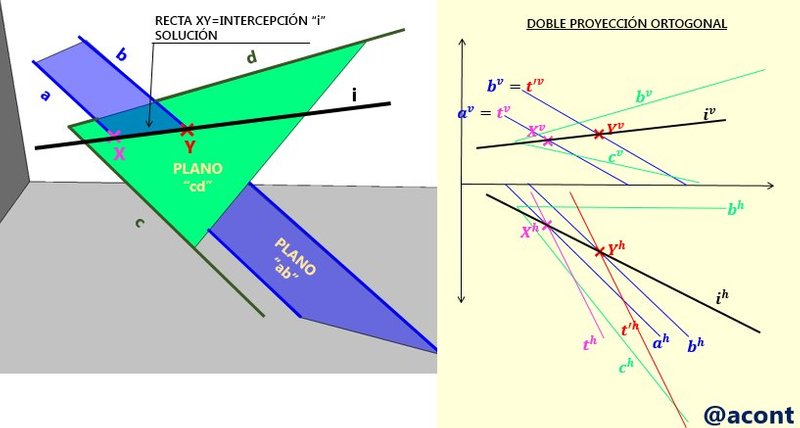
En el siguiente ejemplo, se tiene un plano “ab” dado por dos rectas paralelas “a” y “b”, y un plano “cd” dado por dos rectas “c” y “d” que se cortan. La recta “i” es la solución. (Fig. N°7).

_{Figura N°7}

En la DPO se observaría lo siguiente (Fig. N°8).

_{Figura N°8}

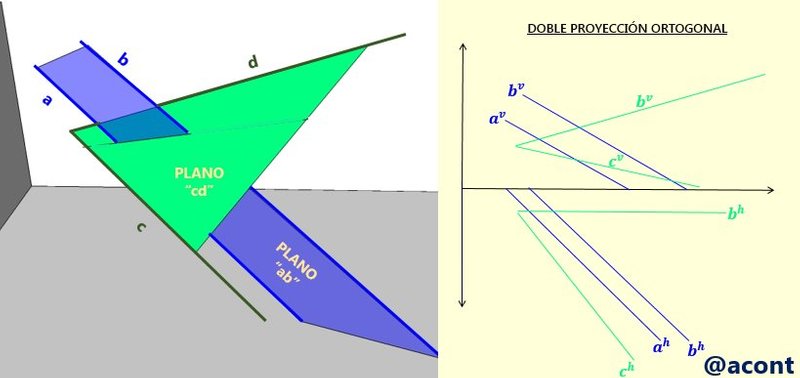
Para determinar las proyecciones de “i” en la DPO, podemos tomar dos rectas (por ejemplo, las del plano “ab”) e interceptarlas con el plano “cd” para así encontrar dos puntos por los cuales trazar la recta de intercepción entre ambos planos.

Primero vamos a hallar la intercepción de la recta “a” con el plano “cd”. Esto lo realizamos de forma similar al procedimiento realizado anteriormente. Vamos a determinar una recta adicional “t” del plano “cd” la cual coincide con la recta “a” en su proyección vertical, y hallaremos su proyección horizontal mediante líneas de referencia verticales a partir del punto de corte con las proyecciones verticales de las rectas “c” y “d” (Fig. N°9). De esta manera hallamos un punto de corte “X” entre ambos planos, es decir, de una recta del plano “ab” con el plano “cd”.

_{Figura N°9}

Procederemos de forma similar con la recta “b”. Supondremos una recta adicional “t’” perteneciente al plano “cd”, la cual coincide con la recta “b” en su proyección vertical. Determinando la proyección horizontal de “t’”, hallaremos el punto de corte entre la recta adicional “t’” y “b” (Fig. N°10).

_{Figura N°10}

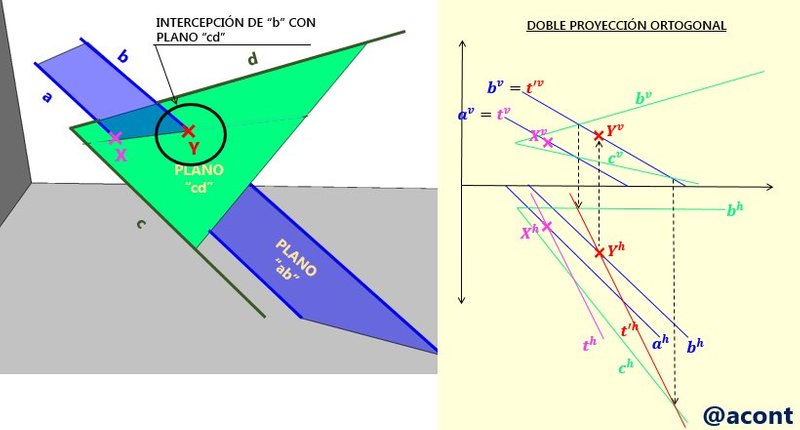
Hemos encontrado dos puntos de corte entre ambos planos, por lo que podemos trazar la intercepción entre ambos (Fig. N°11).

_{Figura N°11}

Hasta ahora hemos hallado la intersección entre dos planos cualquiera. Pero también podemos encontrar la intercepción entre dos planos dados por sus trazas (es decir, sus rectas características) (Fig. N°12).

_{Figura N°12}

En este caso, no es necesario determinar rectas adicionales, ya que el punto de corte entre dos trazas de ambos planos nos da directamente un punto por donde la recta de intercepción va a pasar.

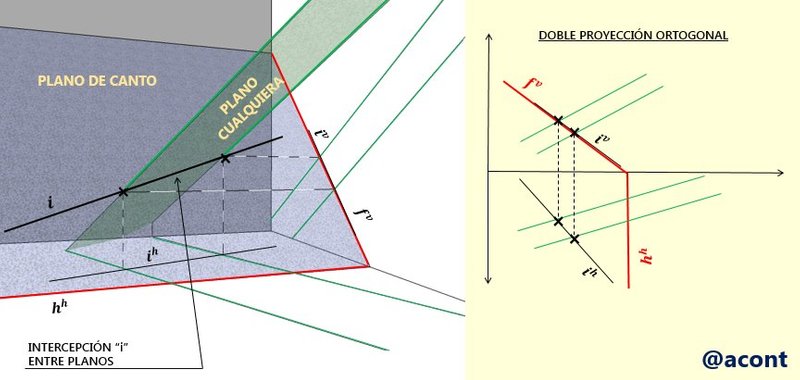
Al igual que en el caso de la intercepción de rectas con planos, los planos de canto y plano vertical nos brindan directamente su intercepción con otro plano cualquiera, puesto que en la DPO el punto de corte se refleja directamente en una de sus proyecciones. Para ilustrar esto, se muestra un ejemplo de intersección entre un plano vertical con un plano cualquiera “ab” (Fig. N°13).

_{Figura N°13}

Aportes de esta publicación

Encontrar la intercepción de los planos con otros objetos tales como rectas y otros planos en la Doble Proyección Ortogonal, requiere de ciertos procedimientos que podrían no entenderse a primera vista, pero con una vista tridimensional de la situación, se puede llegar a comprender el porqué de cada elemento trazado para llegar a la solución requerida. Por ello, mediante el programa SketchUp, se lograr obtener un punto de vista tridimensional del problema, desarrollando así la capacidad para representar objetos del espacio tridimensional en el papel mediante la Doble Proyección Ortogonal.

---

Referencias Bibliográficas

•Osers et al (2012). Estudio de Geometría Descriptiva (14va Edición). Editorial Torino. Caracas._{Fuente para consulta (doceava edición)}

Material recomendado

•Di Pietro, Donato (1985). Geometría Descriptiva. Editorial Alsina. Buenos Aires.

•Izquierdo Asensi, F (1957). Geometría Descriptiva. Editorial Paraninfo. Madrid.

---

Imágenes de autoría propia, realizadas mediante el programa SketchUp 8 y posteriormente editadas con Microsoft PowerPoint.

---

Publicado mediante STEM.OpenHIVE

Visite la etiqueta #STEM-espanol para encontrar contenido de calidad en habla hispana referente a Ciencias, Tecnología, Ingeniería, Matemáticas y otros tópicos relacionados. @STEM-espanol es una comunidad dedicada a la difusión de contenido en español referente a STEM (ciencia, tecnología, ingeniería y matemáticas por sus siglas en inglés) conformada por autores de todo el mundo.

_{Para mayor información y si deseas publicar contenido STEM acá está el enlace de invitación al canal de Discord de #STEM-espanol donde puedes presentarte y aclarar dudas: https://discord.gg/UJwQXWP}

HiveSTEM (nombre provisional, puede votar por el nuevo nombre a través de este enlace) es un proyecto en la plataforma Hive al cual #STEM-espanol está adscrito, cuyo objetivo es implementar un medio de comunicación STEM en Hive.

---

_{Ing. Angel Contreras}